Brachistochrone

Quite Start

Background

The problem of the quickest descending line or shortcut is the first variational problem to appear in history and is a sign of the development of variational methods. The problem was proposed by John Bernoulli in 1696 in an open letter to his brother Jacob Bernoulli. The formulation of the problem is: let A and B are not in the same lead plane on the two points, in all the plane curve connecting A and B, to find a curve, so that only by gravity and the initial speed of the zero point from point A to point B along the curve of the shortest time required to move!

---

Demand

Using DP ways to solve this problem. Discrete this as grids, from the end to the start, calculate the faastest ways needs shortest times.

---

Mathematical Model

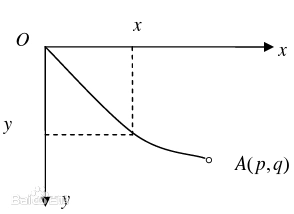Let the curve be y=y(x) with coordinates as shown in Fig. 1, the mass starts moving from point O, its velocity v is related to its longitudinal coordinate:

$v=\sqrt{2gy}$
At the point (x, y) on the curve, the velocity of the mass point is

$v=\frac{ds}{dt}=\sqrt{1+y^{\mathrm{\prime }2}}\frac{dx}{dt}$
where s denotes the arc length of the curve and t denotes the time.

Since the transverse coordinates of points O, A are 0, p respectively, the time required for the mass m to move from point O to point A is

$dt=\frac{\sqrt{1+y^{\mathrm{\prime }2}}}{v}dx=\frac{\sqrt{1+y^{\mathrm{\prime }2}}}{\sqrt{2gy}}dx$
In this way, the time t required for the mass to move from point O to point A is a function of y(x), and the fastest descending line problem is one that satisfies the boundary conditions of

$t=J(y)={\int }_0^b \frac{\sqrt{1+y^{\mathrm{\prime }2}}}{\sqrt{2gy}}dx$
Of all the continuous functions y(x), find the one function y that minimises the generalised function.
$y\left(\mathrm{(0)}\right)=0,y\left(\mathrm{(b)}\right)=h$

Main Code in Python